In this post, I will explain how to interpret Grim Dawn’s game database files to find out what the drop rate for a specific combination of affixes is.
Disclaimer: while this procedure is based on actual game data, it uses my current theory about how the game probably interprets that data. It’s quite possible I’m wrong. But I believe the theory because the game’s files are descriptive enough that they strongly suggest this is the correct interpretation, and because the outcomes of the procedure seem to resemble observed frequencies. But people are really bad at estimating this sort of thing, so we don’t have good data on observed frequency! (We do have some data, though.) If anyone has an alternative theory or evidence that I’m wrong, I’d love to hear it!
We’ll use an example to step through the process and illustrate how it works. One of my characters uses the Evoker Vindicator build that’s #5 on the patch 1.1.9 top 20 builds list. That build uses a couple green items, including a Thunderstruck Moosilauke’s Pauldron’s of Squalls. That will be our example, and the question we’ll be asking is: how rare is that affix combination?
Loot Table files
The first step is to find the loot table for the item you’re interested in. The game’s database files actually contain three separate loot tables for Moosilauke’s MIs.
records/items/loottables/gearshoulders/tdyn_shoulders_b12_nemesisundead_01.dbr
records/items/loottables/gearshoulders/tdyn_shoulders_b12_nemesisundead_02.dbr
records/items/loottables/gearshoulders/tdyn_shoulders_b12_nemesisundead_03.dbr
And there are five different versions of Moosilauke’s Pauldrons, each with a different item level
level database file
50 records/items/gearshoulders/b019a_shoulder.dbr
65 records/items/gearshoulders/b019b_shoulder.dbr
75 records/items/gearshoulders/b019c_shoulder.dbr
84 records/items/gearshoulders/b019d_shoulder.dbr
94 records/items/gearshoulders/b019e_shoulder.dbr
The different loot tables have different weights for these variations of the item. I’m not entirely sure which loot table is used where – I think 01 is used for drops from Moosilauke himself, and probably 03 is for SR loot chests? But I’m not sure about that. The main difference seems to be that 01 can drop lower level versions of these items if Moosi’s level is low enough, but 03 can’t (so presumably it’s only used in some context where we already assume max level).
Fortunately, we can ignore most of that complexity. Inspecting the loot tables, we see that those files contain weights for affix combinations and different prefix and suffix tables, not the item files. And all three loot tables for Moosi’s shoulders have the same affix weights. Interestingly, the tables also contain entries both for Moosi’s Pauldrons and Moosi’s Shoulderguards, which indicates that both items have identical probabilities for different affix combinations. So, we simplify away all this complexity by restricting ourselves to the question: assuming we see a max level Moosilauke’s Pauldrons drop, what is the chance that it drops with both Thunderstruck and of Squalls?
Affix Combos
So now how do we use the loot table to determine the probabilities of different affixes? There are two pieces to this: the affix combo and the prefix and suffix tables. We’ll cover the affix combo first.
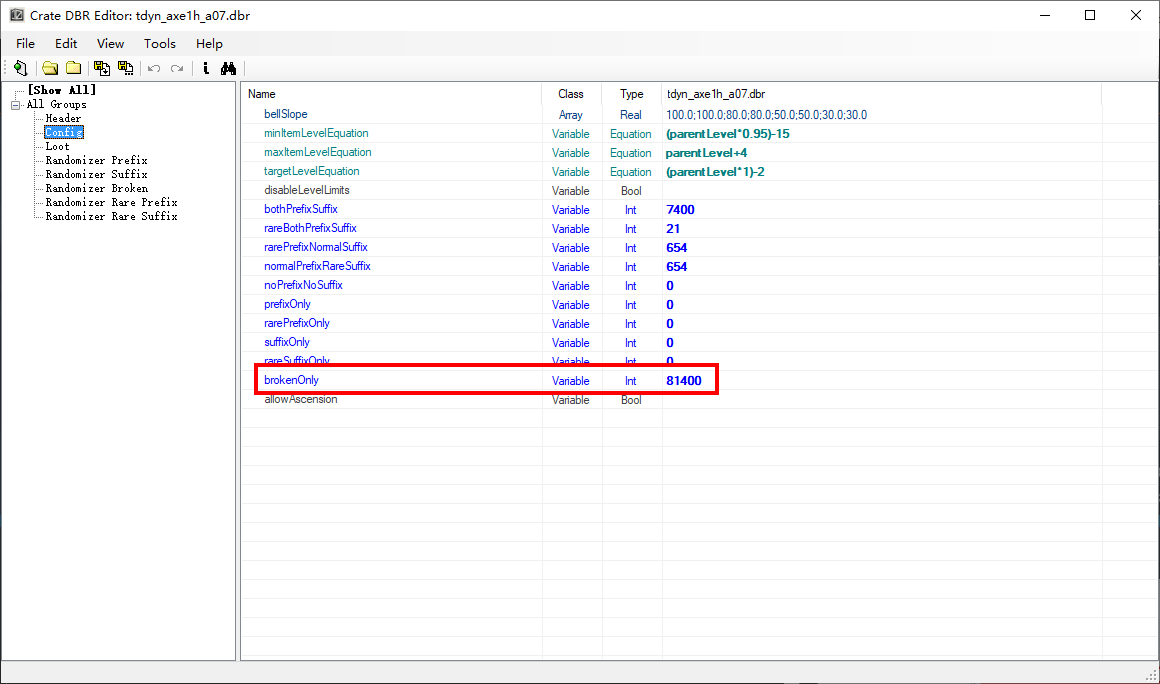
Each loot table file lists weights for 10 different affix combo possibilities. Here they are for Moosi’s shoulders:
combo weight
bothPrefixSuffix 0
brokenOnly 0
noPrefixNoSuffix 0
normalPrefixRareSuffix 475
prefixOnly 0
rareBothPrefixSuffix 50
rarePrefixNormalSuffix 475
rarePrefixOnly 0
rareSuffixOnly 0
suffixOnly 0
If you’re wondering what “brokenOnly” means, I think that’s there because Grim Dawn has a what-you-see-is-what-you-get loot system, which means that for some items, monsters can actually equip and use them, and they will be visible in the game, and the monster will drop that item. But sometimes there’s a chance that the item you see doesn’t drop, because it’s “broken”. Anyway, this category has a 0 weight for the item we’re interested in, so even if that’s wrong it won’t affect our analysis.
Back to our main question, we can observe by inspecting other loot tables that nemesis shoulders all have these same weights. Notice a couple things about them:
- They sum to 1,000, so you can easily convert to a percentage by dividing by 10 (this isn’t true on every loot table, but it is here).
- Only three categories have non-zero weight, and all of these are for rare affixes. So nemesis shoulders are guaranteed to have at least one rare affix (which matches observed frequency, in my experience).
- The file contains different affix tables for prefix and rare prefix, and likewise for suffix and rare suffix. That suggests that, to roll for an affix, we need to know first if we’re rolling for a rare or a magic affix. That implies that the affix combo is rolled first, and only then do we roll for specific affixes.
Modifiers
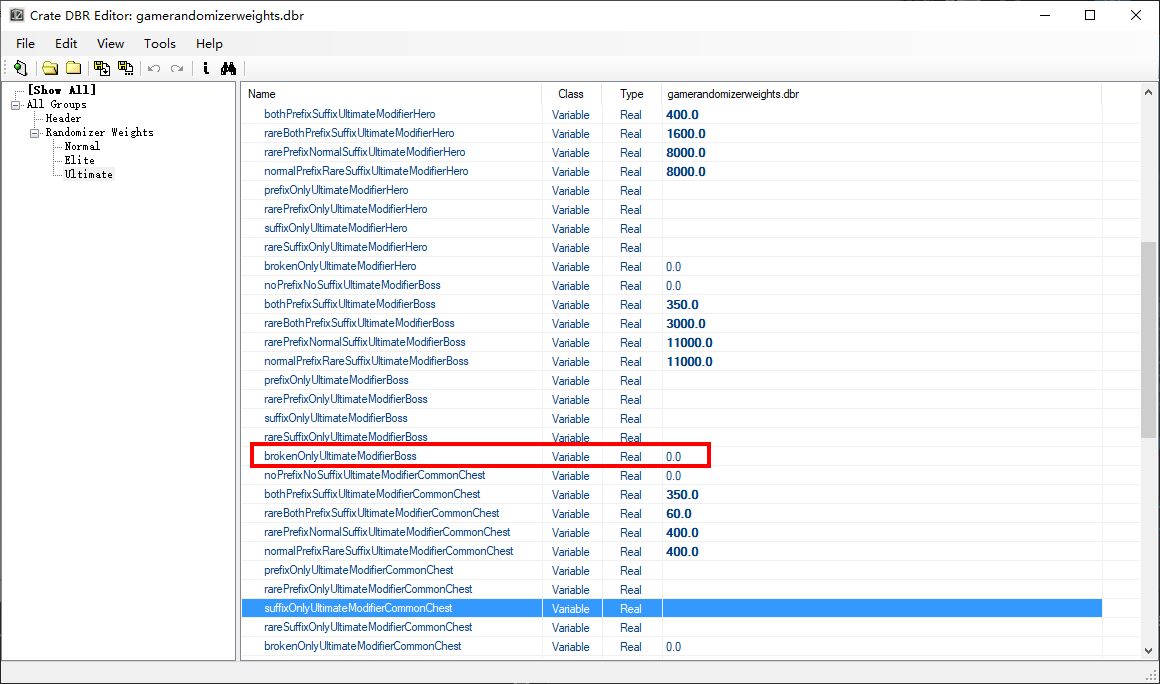
The first time I looked at these files, I assumed that the rates were just what we see in the loot table, so that if you see a Moosilauke’s Pauldrons, it has a 5% chance to have two rare affixes. That was a mistake! It turns out that these weights are modified by two factors: the difficulty, and the source of the drop. These modifiers are laid out in records/game/gamerandomizerweights.dbr, which contains entries like
normalPrefixRareSuffixUltimateModifierBoss,40000.000000,
normalPrefixRareSuffixUltimateModifierBossChest,45000.000000,
normalPrefixRareSuffixUltimateModifierChampion,750.000000,
normalPrefixRareSuffixUltimateModifierChampionChest,3000.000000,
So to get specific drop chances, we’ll need to make more assumptions. So let’s further restrict our question to this: if we see Moosilauke (a boss) drop a max level Moosilauke’s Pauldrons on Ultimate difficulty, what is the chance that it drops with both Thunderstruck and of Squalls?
Let’s call the weights in the loot table the “base weights”. Then we also need to make some assumptions about how these modifiers are combined with the base weights. I looked at two different hypotheses: additive and multiplicative. These are just what they sound like – the additive hypothesis is that the modifier is added to the base weight, and multiplicative is that the two numbers are multiplied together.
I believe the multiplicative hypothesis is correct, for a couple of reasons:
- The chance for two rare affixes from from a nemesis MI drop on Ultimate is 0.52% under multiplicative, and 4.76% under additive. 0.52% seems much closer to reality.
- If additive is correct, the double magic affix weight for nemesis shoulders would be non-zero, which we know is wrong. Therefore, either multiplicative is correct, or the true rule is a modified version of additive with a special case for when the base rate is 0. That means multiplicative is the simplest hypothesis that explains the observed frequencies.
So to get the true chance for a double rare, you’d calculate
rareBothPrefixSuffix * rareBothPrefixSuffixUltimateModifierBoss
---------------------------------------------------------------
SUM(affixComboBaseWeight * affixComboUltimateModifierBoss)
Again, for Moosilauke’s Pauldron’s dropping from a boss on ultimate, that gives us a 0.52% chance for two rare affixes.
Challenge Layers
The last section was an oversimplification. Grim Dawn has “challenge layers” that affect affix combo chances, making rare affixes generally more likely. These are areas with mutators, like roguelike dungeons and SR, or East Marsh. These challenge layers have their own modifiers, defined in records/game/challengelayers/. So we need to consider where Moosi’s Pauldrons are dropping. If we kill Moosi inside the Steps of Torment roguelike dungeon, the chances of rare/rare affix combo increases to 0.63%.
However, the best way to farm nemesis items these days seems to be SR runs, and it turns out that Moosi’s Pauldron’s dropped from a Boss Chest in an Endless Dungeon treasure room have exactly the same 0.52% rare/rare chance as when Moosi himself drops them in a normal zone (no mutators). So we’ll use that chance for our calculations here.
Affix Tables
Once we’ve gotten lucky enough to roll that 0.52% chance, we still have to narrow it down to a the specific affixes we’re looking for. To do that, we need to know which affix table to roll on. The loot table will have one or more rarePrefixTable and rareSuffixTable entries, each of which has both a weight and a min and max level. I assume that, if Moosilauke’s level is not between the min and max level for a table, the chance of rolling on that table is 0. So we filter those out, then generate a chance for each table equal to its weight divided by the sum of the weights for all max level tables.
For the Moosilauke’s shoulders loot table, for example, there are two rare prefix tables and three rare suffix tables. However, for both prefix and suffix only a single table has a max level greater than 70, so we are always going to be rolling on that table. If we were rolling for a level 70 Moosilauke, we’d have some non-zero chance to roll from each of more than one table. But we can, again, ignore that complexity by assuming max level.
So we are rolling once on both of the following two tables:
records/items/lootaffixes/prefix/prefixtables/prefixb02_armor_all.dbr
records/items/lootaffixes/suffix/suffixtables/suffixb02_armor_all.dbr
These tables are pretty simple. They’re just lists of “randomizers”, which just means a specific affix, again with a level range and a weight. So we perform the same procedure: filter out all randomizers with a level range that doesn’t include our max level item, then divide the weight for an individual randomzier with the sum of the weights of all max level randomizers. That gives us the probability that we roll a specific affix, given that we are already rolling on this specific affix table.
If you’re following along in the game files, the tricky part here is that each “randomizer” is a reference to another game file, and you have to follow that reference that then resolve the text tag or look at the bonuses it gives in order to figure out which affix is which. This is annoying to do manually, so I automated the process for myself.
The rare prefix table used by Moosi’s shoulders has 25 different outcomes. They aren’t equally likely – chances for a given affix range from 2.2% to 4.5%. Thunderstruck in particular has a 3.8% chance, if we’re rolling on this table. On the suffix table, of Squalls is less likely, because there are 35 different suffixes we might roll – it’s only a 2.8% chance.
Drop Chance
Now we have everything that we need to compute the probability of getting a Thunderstruck Moosilauke’s Pauldrons of Squalls. Let 2R be the chance of getting two rare affixes, T is the probability of Thunderstruck on table prefixb02_armor_all, and S is the probability of of Squalls on table suffixb02_armor_all. These rolls are all independent – we roll affix combo first, then we roll to determine which affix table to roll on (for each of prefix and suffix), then we roll within the affix table to determine the specific affix. In our case, we can just ignore the affix table chance, because there’s only one prefix table and one suffix table. So the probability of a Thunderstruck Moosilauke’s Pauldron’s of Squalls (given a max level drop from SR on Ultimate) is just
p(2R & T & S) = p(2R)p(T)p(S) = 0.0052 * 0.038 * 0.028 = 0.0000056
That’s 0.00056%, or about 1 in 200,000.
Bonus Calculation
It’s hard to know how to interpret numbers like these. A useful calculation is the probability that you will have seen at least one event e in n trials.
p(at least one e) = 1 - (1 - p(e))^n
For example, since Moosi only has a 50% chance to drop Pauldrons rather than Shoulders, if you kill him 100 times, the probability that you’d have seen at least one Thunderstruck Pauldrons of Squalls is
1 - (1 - 0.0000056 * 0.5)^100 = 0.00028
or 0.028%, about 1 in 3,500.
And we can take that further. If you run SR over and over, how many Moosi’s Pauldron’s should you expect to see before it drops with these affixes? Well, there’s going to be a lot of variance here, but we can ask, if billions and billions of people did this, how many drops would it take them on average?
The answer to that is: whatever the n value we could plug into the equation above to get a probability of 50%. We can compute that using logarithmic identities:
0.5 = 1 - (1 - 0.0000056 * 0.5)^n
0.5 = (1 - 0.0000056 * 0.5)^n
ln(0.5) = n * ln(1 - 0.0000056 * 0.5)
n = ln(0.5) / ln(1 - 0.0000056 * 0.5)
n = 245,961
So we’d expect to see 245,961 drops of Moosi’s Pauldrons in SR, on average, to see a Thunderstruck Pauldrons of Squalls. Important caveat, again, is that there’s a ton of variance – 10% of people would get it in 37,387 drops or fewer (lucky!). But on the other hand, 10% of people would see 817,066 Pauldrons and still never get the affixes they’re after (unlucky!).
Bonus Example: Overseer’s Milton’s Casque
I don’t want to give the impression that the point of all this is to show that green items are ultra-rare and you shouldn’t ever attempt to farm them. That’s not the case! Let me provide an example from @mad_lee 's Blitz Warlord build. That build really wants an Overseer’s Milton’s Casque, but can be flexible on the suffix. So how rare is an Overseer’s Milton’s Casque?
Milton always drops his casque (since 1.2), and since he’s a Boss, on Ultimate he has a very good chance to drop a rare prefix. Overall, let C be “Milton dropped his casque”, R be “Milton’s casque has a rare prefix (on Ultimate, dropping from a Boss, with no mutators)”, and O be “The prefix is Overseer’s”. Then likelihood that a kill of Milton Heart drops an Overseer’s Casque (on Ultimate) is
p(C)p(R)p(O|R)
As noted, p(C) is 1. p(R) is a bit different than for a nemesis drop, because the affix combo weights are different (notably, there’s a non-zero chance to roll both non-rare affixes, and the double rare chance is actually a little bit higher). But the procedure for computing it is the same – we sum the modified weights of the two affix combo categories that grant a rare prefix and divide by the sum total of all modified affix combo weights in the loot table. Also, we know Milton always spawns in a normal area – no mutators. So we use the base Boss, Ultimate modifiers rather than the ones from any challenge layer.
Milton’s Casque has more than one rare prefix table, and Overseer’s only appears on one of those tables (the head armor table). Let H be “we’re rolling on the head armor table”. Then p(O|R) = p(H|R)p(O|H). We can calculate p(O|H) just by the usual procedure of dividing the weight for max level Overseer’s by the total weight of max level affixes on that table, and p(H|R) by dividing the table weight by the sum of the (max level) affix table weights in the loot table. Substituting these numbers, we get:
1 * 0.452 * 0.417 * 0.460 = 0.0866
or 8.66%. Those are pretty good odds, and plugging that into our expected kills formula that means you only expect to have to kill Milton 9 times, on average, to see an Overseer’s Milton’s Casque. The luckiest 10% of people will get it on their first try! The unluckiest 10% of people will have to kill him 25 times or more, but that still won’t take too long (Milton’s also quick to find). This is an easily farmable drop.
Conclusion
I hope you’ve enjoyed this peek behind the curtain. I also hope anyone who spots an error in my math or my assumptions, or who has evidence that my interpretation of the database files is incorrect, will let me know. Thanks for reading!
)